 初中數學八年級下冊第5章特殊平行四邊形5.1矩形教案新版浙教版.doc
初中數學八年級下冊第5章特殊平行四邊形5.1矩形教案新版浙教版.doc
5.1 矩形學習目標知識與技能:1.探索并掌握矩形的有關性質,領會矩形的內涵.2.理解并掌握矩形的判定方法.3.會利用矩形的判定方法進行簡單的證明.過程與方法:經歷探索矩形有關性質和矩形的判定過程,在直觀操作活動中學會簡單說理,發展初步的合情推理能力和主動探究習慣,逐步掌握說理的基本方法學習難點理解和掌握矩形的性質和判定方法,發展合情推理能力和主動探究習慣教學過程一、回顧.1平行四邊形有哪些性質?2有幾種方法可以識別四邊形是平行四邊形?3平行四邊形是中心對稱圖形嗎?它的對稱中心是什么樣的點?平行四邊形是軸對稱圖形嗎?如果是,它的對稱軸是怎樣的直線?如果不是,請說明理由二、創設問題情境,引入新課.1教師出示教具:“一個活動的平行四邊形木框”,用兩根橡皮筋分別套在相對的兩個頂點上拉動一對不相鄰的頂點A,C,立即改變平行四邊形的形狀,如圖學生思考如下問題:(1)無論如何變化,四邊形ABCD還是平行四邊形嗎?(2)隨著的變化,兩條對角線的長度有沒有變化?學生憑直覺可以很快地回答上述問題隨著由銳角變成鈍角時,過頂角的對角線由長變短,而另一條對角線由短變長當是銳角時,學生可以用刻度尺量出兩條對角線的長度,你可判別它們數量之間的關系嗎?當是鈍角時,學生也可以用同樣的辦法,得到兩對角線的數量關系(3)當為直角時,這個時候平行四邊形就變成一個特殊的平行四邊形矩形這就是你們以前學過的長方形教師根據學生的回答,板書:矩形這就是我們今天著手研究的一個課題(4)那怎樣的平行四邊形是矩形呢?2同學回答,老師板書:有一個內角為直角的平行四邊形是矩形?如果人家問怎樣的四邊形是矩形呢?那就要說四個內角都是直角(或三個內角都是直角)的四邊形是矩形大家想一想矩形是平行四邊形嗎?(是)那么矩形就具有平行四邊形的一切性質即矩形是中心對稱圖形;對邊分別平行;兩組對邊分別相等;兩組對角分別相等;對角線互相平分3矩形除了以上性質外,還有它的特有的性質嗎?學生思考以下問題:(1)上面的活動架當為直角時,它們的對角線有何關系?(2)矩形是軸對稱圖形嗎?如果是,它的對稱軸是怎樣的直線?如果不是請說明理由(3)說出日常生活中的矩形圖象4讓我們一起來歸納矩形的性質,并板書:(1)矩形具有平行四邊形的一切性質(2)矩形是軸對稱圖形(3)矩形的對角線相等(4)矩形的四個角都是直角思考:(1)平行四邊形的判定方法除定義外,還有哪幾種判定方法?(2)這些判定方法是通過什么方法得到的?(平行四邊形的性質定理的逆命題,猜測、驗證、邏輯推理得到的)5.你能根據矩形特有性質猜想出矩形的判定方法嗎?猜想結論:(1)有三個角是直角的四邊形是矩形;(2)對角線相等的平行四邊形是矩形.這兩個猜想正確嗎?畫圖驗證.演繹推理證明:(1)有三個角是直角的四邊形是矩形.已知:在四邊形ABCD中,A=B=C=90,求證:四邊形ABCD是矩形.(教師引導學生證明,先證這個四邊形是平行四邊形,再利用有一個角是直角的平行四邊形是矩形證明.學生獨立完成)(2)對角線相等的平行四邊形是矩形.(引導學生證明這個四邊形有一個角是直角)歸納:矩形的判定方法:判定定理1 有三個角是直角的四邊形是矩形.判定定理2 對角線相等的平行四邊形是矩形.歸納后,讓學生說出這兩個判定定理的不同.三、例題講解.例1 已知:如圖,矩形ABCD的對角線AC,BD相交于點O,AOD=120,AB=4 cm.(1)判斷AOB的形狀.(2)求矩形的對角線的長.例2 如圖,一張四邊形紙板ABCD的兩條對角線互相垂直.若要從這張紙板中剪出一個矩形,并使它的四個頂點分別落在四邊形ABCD的四條邊上,可怎樣剪?四、全課小結,提高認識.矩形的定義:有一個角是直角的平行四邊形叫做矩形.矩形的性質:矩形的四個角都是直角.矩形的對角線相等.矩形的判定:有三個角是直角的四邊形是矩形.對角線相等的四邊形是矩形
- 關 鍵 詞:
- 初中 數學 年級 下冊 特殊 平行四邊形 5.1 矩形 教案 新版 浙教版
 叮當云教育所有資源均是用戶自行上傳分享,僅供網友學習交流,未經上傳用戶書面授權,請勿作他用。
叮當云教育所有資源均是用戶自行上傳分享,僅供網友學習交流,未經上傳用戶書面授權,請勿作他用。 關于本文
相關資源
 初中數學八年級下冊第4章平行四邊形4.3中心對稱教案新版浙教版.doc
初中數學八年級下冊第4章平行四邊形4.3中心對稱教案新版浙教版.doc  初中數學八年級下冊第4章平行四邊形4.5三角形的中位線教案新版浙教版.doc
初中數學八年級下冊第4章平行四邊形4.5三角形的中位線教案新版浙教版.doc  初中數學八年級下冊第1章二次根式1.3二次根式的運算教案新版浙教版.doc
初中數學八年級下冊第1章二次根式1.3二次根式的運算教案新版浙教版.doc  初中數學八年級下冊第2章一元二次方程2.2一元二次方程的解法教案新版浙教版.doc
初中數學八年級下冊第2章一元二次方程2.2一元二次方程的解法教案新版浙教版.doc  初中數學八年級下冊第5章特殊平行四邊形5.2菱形教案新版浙教版.doc
初中數學八年級下冊第5章特殊平行四邊形5.2菱形教案新版浙教版.doc  初中數學八年級下冊第6章反比例函數6.3反比例函數的應用教案新版浙教版.doc
初中數學八年級下冊第6章反比例函數6.3反比例函數的應用教案新版浙教版.doc  初中數學八年級下冊第6章反比例函數6.2反比例函數的圖象和性質教案新版浙教版.doc
初中數學八年級下冊第6章反比例函數6.2反比例函數的圖象和性質教案新版浙教版.doc  初中數學八年級下冊第5章特殊平行四邊形5.3正方形教案新版浙教版.doc
初中數學八年級下冊第5章特殊平行四邊形5.3正方形教案新版浙教版.doc  初中數學八年級下冊第3章數據分析初步3.1平均數教案新版浙教版.doc
初中數學八年級下冊第3章數據分析初步3.1平均數教案新版浙教版.doc  初中數學八年級下冊第4章平行四邊形4.2平行四邊形及其性質教案新版浙教版.doc
初中數學八年級下冊第4章平行四邊形4.2平行四邊形及其性質教案新版浙教版.doc 


 譯林版五年級上英語Project 1 參考教案.doc
譯林版五年級上英語Project 1 參考教案.doc  譯林版五年級上英語Unit 1 第2課時教學設計.doc
譯林版五年級上英語Unit 1 第2課時教學設計.doc  譯林版五年級上英語Project 2 參考教案.docx
譯林版五年級上英語Project 2 參考教案.docx  譯林版五年級上英語Unit 1 第3課時教學設計.doc
譯林版五年級上英語Unit 1 第3課時教學設計.doc  譯林版五年級上英語Unit 1 第4課時教學設計.doc
譯林版五年級上英語Unit 1 第4課時教學設計.doc  譯林版五年級上英語Unit 1 第1課時教學設計.doc
譯林版五年級上英語Unit 1 第1課時教學設計.doc  譯林版五年級上英語Unit 2知識點梳理+重難點鞏固提優.docx
譯林版五年級上英語Unit 2知識點梳理+重難點鞏固提優.docx  譯林版五年級上冊英語知識點總結+梳理.docx
譯林版五年級上冊英語知識點總結+梳理.docx  譯林版五年級上英語Unit 7 第1課時參考教案.docx
譯林版五年級上英語Unit 7 第1課時參考教案.docx  譯林版五年級上英語Unit 6 第3課時參考教案.docx
譯林版五年級上英語Unit 6 第3課時參考教案.docx  譯林版五年級上英語Unit 4 第3課時參考教案.docx
譯林版五年級上英語Unit 4 第3課時參考教案.docx  譯林版五年級上英語Unit 4 第1課時參考教案.docx
譯林版五年級上英語Unit 4 第1課時參考教案.docx  譯林版五年級上英語Unit 2 第3課時教學設計.doc
譯林版五年級上英語Unit 2 第3課時教學設計.doc  譯林版五年級上英語Unit 2 第1課時教學設計.doc
譯林版五年級上英語Unit 2 第1課時教學設計.doc  譯林版五年級上英語Unit 4知識點梳理+重難點鞏固提優.docx
譯林版五年級上英語Unit 4知識點梳理+重難點鞏固提優.docx  譯林版五年級上英語Unit 1知識點梳理+重難點鞏固提優.docx
譯林版五年級上英語Unit 1知識點梳理+重難點鞏固提優.docx  2025秋人教版八年級上冊英語Unit 2 Home Sweet Home Section A(2a-2e)課件(共36張PPT).pptx
2025秋人教版八年級上冊英語Unit 2 Home Sweet Home Section A(2a-2e)課件(共36張PPT).pptx  2025秋人教版八年級上冊英語Unit 1 Happy Holiday Section B (1a-1d) 課件.pptx
2025秋人教版八年級上冊英語Unit 1 Happy Holiday Section B (1a-1d) 課件.pptx  2025秋人教版八年級上冊英語Unit 1單詞講解課件.pptx
2025秋人教版八年級上冊英語Unit 1單詞講解課件.pptx  2025秋人教版八年級上冊英語Unit 2 Home Sweet Home 語境學單詞.docx
2025秋人教版八年級上冊英語Unit 2 Home Sweet Home 語境學單詞.docx  2025秋人教版八年級上冊英語Unit 1 Section A (1a-1d)課件.pptx
2025秋人教版八年級上冊英語Unit 1 Section A (1a-1d)課件.pptx  2025秋人教版八年級上冊英語Unit 2 Home Sweet Home Section B(3a-Reflecting)課件(共43張PPT).pptx
2025秋人教版八年級上冊英語Unit 2 Home Sweet Home Section B(3a-Reflecting)課件(共43張PPT).pptx  2025秋人教版八年級上冊英語單元語法Unit 5.pdf
2025秋人教版八年級上冊英語單元語法Unit 5.pdf  2025秋人教版八年級上冊英語單元語法Unit 8鞏固練習.pdf
2025秋人教版八年級上冊英語單元語法Unit 8鞏固練習.pdf  2025秋人教版八年級上冊英語Unit 5 What a Delicious Meal!語境學單詞.docx
2025秋人教版八年級上冊英語Unit 5 What a Delicious Meal!語境學單詞.docx 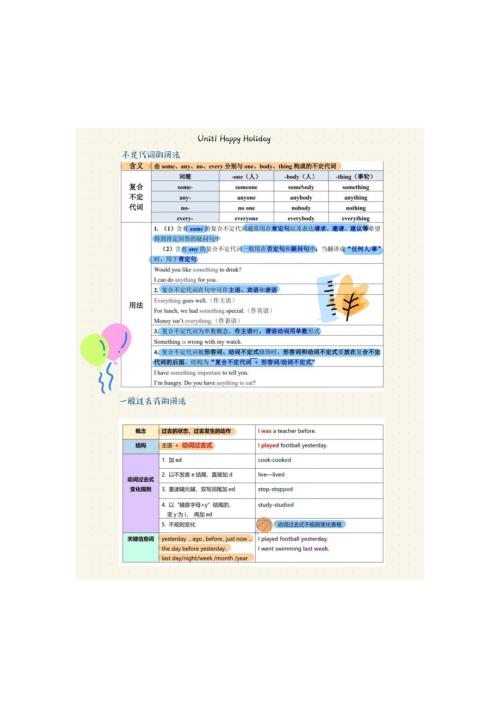 2025秋人教版八年級上冊英語全冊語法總結.pdf
2025秋人教版八年級上冊英語全冊語法總結.pdf  2025秋人教版八年級上冊英語講義Unit 1-8(教師版).pdf
2025秋人教版八年級上冊英語講義Unit 1-8(教師版).pdf  2025秋人教版八年級上冊英語Unit 1 Happy Holiday 語境學單詞 .docx
2025秋人教版八年級上冊英語Unit 1 Happy Holiday 語境學單詞 .docx  2025秋人教版八年級上冊英語單元語法Unit 3鞏固練習.pdf
2025秋人教版八年級上冊英語單元語法Unit 3鞏固練習.pdf  2025秋人教版八年級上冊英語Unit 2 Home Sweet Home Section B(1a-2c)課件(共39張PPT).pptx
2025秋人教版八年級上冊英語Unit 2 Home Sweet Home Section B(1a-2c)課件(共39張PPT).pptx  2025秋人教版八年級上冊英語單元語法Unit 6鞏固練習.pdf
2025秋人教版八年級上冊英語單元語法Unit 6鞏固練習.pdf 

